Thành phần không đoán được, dzt nhân với b(t) được gọi là “khuếch tán”. “Không đoán được” có nghĩa là vào thời điểm t, độ khuếch tán không được xác định từ những thông tin trong quá khứ. Định nghĩa quá trình cần một phân phối cho độ khuếch tán.
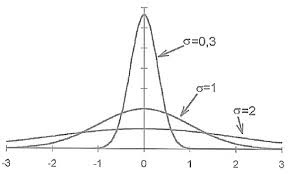
Biến số £ có phân phối chuẩn chuẩn hóa, tức là 0(0,1). Đó là thừa số ngẫu nhiên ẩn trong z. Nhưng thừa số z ngẫu nhiên không có phương sai đơn vị. Với một quá trinh như vậy, phương sai có dạng ơ 2(t)At và độ lệch chuẩn là Ơ’(/)VÃ7. Điều đó cho phép phương sai phụ thuộc vào thời gian và tỷ lệ thuận với khoảng thời gian.
Thừa số ngẫu nhiên có một số tính chất đặc biệt. E[ Azt ]2 là phương sai vì giá trị kỳ vọng của Azt bằng 0. Phương sai là “độ lớn của Azt 2 điển hình. Giả sử bình phương này không đáng kể đổng nghĩa với giả sử phương sai bằng 0. Quá trình sẽ trở nên tất định. Azt có phương sai tỷ lệ thuận với At.
Để đi từ thời điểm 0 tói T, chúng ta tích lũy những biến đổi của những khoảng thời gian ròi rạc giữa 0 và T. Giá trị cuối cùng tích lũy những biến đổi ngẫu nhiên. Giữa ngày hiện tại và tương lai, quá trình tuân theo một đường thời gian kết nối tất cả những điểm thời gian. Ví dụ về đường thời gian của giá cổ phiêu được minh họa sau khi trình bày những quá trình chính.
Tùy vào biến ngẫu nhiên, giá cổ phiếu, giá trị tài sản của một công ty hay lãi suất, hệ số a(t) và b(t) có nhiều dạng. Những quá trình ngẫu nhiên điển hình sẽ được trình bày chi tiết ở đây.
Biến số £ có phân phối chuẩn chuẩn hóa, tức là 0(0,1). Đó là thừa số ngẫu nhiên ẩn trong z. Nhưng thừa số z ngẫu nhiên không có phương sai đơn vị. Với một quá trinh như vậy, phương sai có dạng ơ 2(t)At và độ lệch chuẩn là Ơ’(/)VÃ7. Điều đó cho phép phương sai phụ thuộc vào thời gian và tỷ lệ thuận với khoảng thời gian.
Thừa số ngẫu nhiên có một số tính chất đặc biệt. E[ Azt ]2 là phương sai vì giá trị kỳ vọng của Azt bằng 0. Phương sai là “độ lớn của Azt 2 điển hình. Giả sử bình phương này không đáng kể đổng nghĩa với giả sử phương sai bằng 0. Quá trình sẽ trở nên tất định. Azt có phương sai tỷ lệ thuận với At.
Để đi từ thời điểm 0 tói T, chúng ta tích lũy những biến đổi của những khoảng thời gian ròi rạc giữa 0 và T. Giá trị cuối cùng tích lũy những biến đổi ngẫu nhiên. Giữa ngày hiện tại và tương lai, quá trình tuân theo một đường thời gian kết nối tất cả những điểm thời gian. Ví dụ về đường thời gian của giá cổ phiêu được minh họa sau khi trình bày những quá trình chính.
Tùy vào biến ngẫu nhiên, giá cổ phiếu, giá trị tài sản của một công ty hay lãi suất, hệ số a(t) và b(t) có nhiều dạng. Những quá trình ngẫu nhiên điển hình sẽ được trình bày chi tiết ở đây.
CÁC QUÁ TRÌNH NGẪU NHIÊN PHỔ BIẾN
Quá trình cơ bản nhất là quá trình YViener. Những quá trình đáng quan tâm khác là quá trình Wiener tổng quát hóa và quá trình Ito. Quá trình giá cổ phiếu là một trường hợp đặc biệt của quá trình Ito. Những quá trình khác như lãi suất và bước nhảy là những phần mở rộng đơn giản. Trong phần sau, quá trình được gọi là St và thừa số khuếch tán. Sự khác biệt của các quá trình bắt nguồn từ định nghĩa các hệ số a (độ trôi) và b (khuếch tán). Một số quá trình cơ bản được miêu tả để minh họa những trường hợp đơn giản. Nhưng những quá trình phổ biến nhất bao gồm Ito ứng dụng cho thu nhập tài sản, quá trình trở lại giá trị trung bình ứng dụng với lãi suất và quá trình bước nhảy ứng dụng cho các sự kiện hiếm.
Quá trình Wiener
Quá trình VViener còn được gọi là chuyển động Brown là quá trình ngẫu nhiên của một biến z(t) sao cho biến đổi ngẫu nhiên là Az(t) = z(t + At) — z(t) = € và € tuân theo một phân phối chuẩn 0(0,1) hay <Ị>(0, ơ). Độ trôi của nó bằng 0. Phương sai của nó là một hằng SỐ trong một đơn vị thời gian. Bởi vì những thay đổi ngẫu nhiên liền kề độc lập với nhau và tuân theo cùng một phân phối, quá trình được gọi là độc lập có cùng phân bố hay i.i.d. Phân phối không thay đổi với thời gian, nghĩa là nó giống nhau dù bắt đẩu ở bất kỳ thời điểm nào.
Chia khoảng thời gian thành n khoảng nhỏ A/= 7 và trong khoảng thời gian [0,T] Az(f)tích lũy từ 0 biến T, ta có tổng n biến chuẩn ngẫu nhiên, bắt đầu từ một giá trị z(0) nào đó vào thời điểm 0.
Giá trị kỳ vọng của Az(/) bằng 0. Giá trị kỳ vọng của thay đổi tích lũy là tổng các giá trị kỳ vọng của từng biến đổi giữa 0 và T đều bằng 0, do đó: E[ Azt ]=0. Chuyển động Brown đi theo một đường hỗn loạn xung quanh giá trị bắt đầu.
Vào mỗi thời điềm, chúng ta đi từ giá trị hiện tại sang giá trị tiếp theo “đột ngột”. Đường
đi liên tục nhưng không ‘mịn’. Nó có thể hình thành bằng cách tạo ra những biến chuẩn chuẩn hóa độc lập. Tích lũy những thay đổi ngẫu nhiên chuẩn chuẩn hóa trong một khoảng thời gian tạo ra đường thời gian của quá trình. Bởi vì quá trình không có độ trôi, đường thời gian thay đổi ngẫu nhiên quanh số 0. Những quá trình khác kết hợp độ trôi với quá trình Wiener cơ bản.
Từ khóa tìm kiếm nhiều: quản lý rủi ro